Interior Angles of a Triangle
CONCEPTS
Triangle Properties
• Sum of angles in a triangle = 180°
• All right triangles have 2 angles < 90° and a 90° angle. They also have a hypotenuse.
Congruent Triangle Properties
• Congruent means the same
• All angles in an equilateral triangle are equal
• If 2 sides of the triangle are equal, the angles opposite of those sides are equal (and vice versa)
• Match letters of 2 triangles to determine which sides are equal (If ∆ABC = ∆DEF, then ∠A = ∠D, ∠B = ∠E, ∠C = ∠F)
Bisector
• A line that divides an angle into 2 equivalent or equal angles
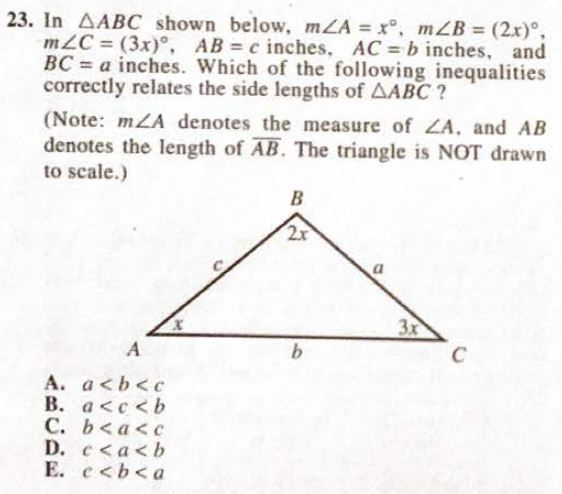
Angles vs Sides
• The largest angles correspond to the largest side in a triangle (and vice versa)
EXAMPLES
• ∠ A has the longest angle, so the side opposite of angle A it has the largest side

PRACTICE PROBLEMS
Question 1 In triangle ABC, the sum of the measures of ∠ A & ∠ B = 29°. What is the measure of ∠ C?
-- Answer -- 151°
∠ C = 180° - (∠ A + ∠ b) = 180° - 29° = 151°
Question 2 What is the degree measure of ∠ BCE (see figure below)?

-- Answer -- 130°
∠ABD = 25° and sides AD = BD so ∠DAB = 25°
Sum of angles in a triangle = 180°, so ∠BDA = 180° - 25° - 25° = 130°
Line ADC = 180° & ∠BDA = 130° so ∠BDC = 180° - 130° = 50°
∠BCD = ∠BDC because opposite sides are congruent. ∠BCE = 180° - ∠BCD = 180° - 50° = 130°
Question 3 The angles in a triangle ABC are ∠ A = 23°, ∠ B = 46° and ∠ C = 111°. Put the sides in order from shortest to longest.
-- Answer -- ∠C > ∠B > ∠A
∠C has the largest angle, so it has the largest side
∠A has the smallest angle, so it has the smallest side
∠C > ∠B > ∠A
Question 4 ∠ A is 50°, ∠ B is 60°. The line extending from A is a bisector. What is the angle on either side of the line (see figure below)?

-- Answer -- 55°
180° - 50° -60° = 110° / 2 = 55°
ACT PRACTICE PROBLEMS